https://openreview.net/forum?id=p14iRzavpt
Introduction
大きなモデルの各サンプルについて、できるだけ推論能力を保ちつつもモデルを小さくする手法として、Knowledge Distillationがある。通常のKDは訓練したモデルとできるだけ同じ分布の出力をするのを目的としているが、
- 教師モデルの学習データのバイアス
- 学習するときに教師モデルの誤った学習
などが原因でうまくない予測をしてしまうことがある。
これに、温度というパラメタを導入して、が1に近いならばlogitがそのまま使われるが、を大きくすると分布がなだらかになり、クラス間の確率差が小さくする、という手法がある。
しかし、このを調節することで得られる効果に限りがあり(なだらかにするだけでは問題を十分に解決できない)し、グリッドサーチでハイパラ調整しないといけない。
この論文では、通常使われているKL-divergenceにマクローリン展開を施し、1次項を摂動として加えるようなKL-Divergenceの改良によって改善を試みる。これは数学的にも正しいとわかっている。
事前知識
一般的な知識蒸留のやり方
Ground Truthラベルがない訓練データセットと、訓練済みの教師モデルが与えられる。これをもとに、学生モデルを訓練する。
この時、以下のようにKLダイバージェンス(経験的に計算)を最小化するのが目的である。
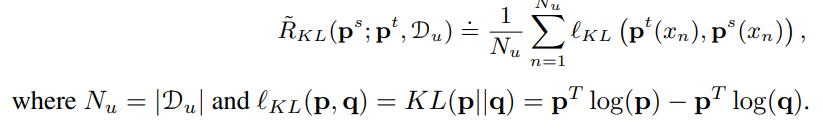
提案手法
教師モデルの出力はground truthのラベルの分布からずれているので、知識蒸留ではKL Divergenceを単に使うだけではうまくいかない。
これを緩めるために、以下のようにKL Divergenceで計算されるを、以下のようにマクローリン展開して、各次元の係数に摂動を加えることで、バイアスがかかってもうまくとらえられるのではないか?
この摂動を加えた対数関数をKL Divergenceの中の「交差エントロピー」で新たに使わせた、新しいKL DivergenceをLossとして、知識蒸留を行う。(エントロピーの部分は据え置く)
KL Divergenceは負のエントロピーと交差エントロピーの差なので、経験的に書き直すと以下のようなる。
ここで、は教師モデル、生徒モデルのそれぞれクラスに対しての予測確率。
このように得たがこの論文の提案したものである。
実際では、無限次数まで級数を計算せず、を設定してそこまで打ち切らせる。
提案手法は、以下のように教師のモデルの出力をKL Divergenceで評価するよりもさらに平滑化させることができるとわかる。
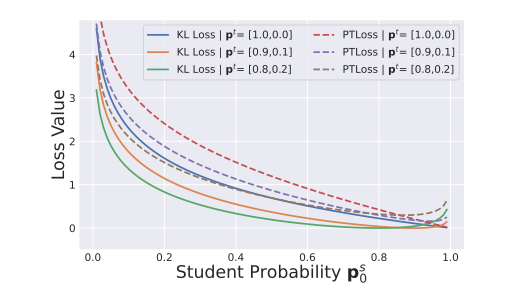
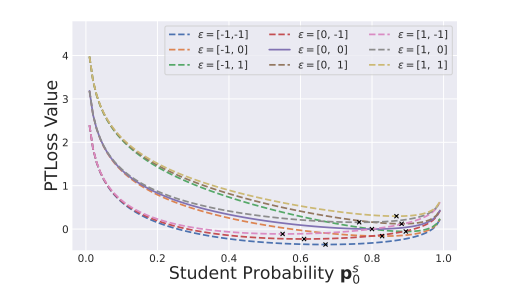
そのうえ、以下のように摂動のを変更することで損失曲線を柔軟に操縦できるとわかる。
提案手法の理論的根拠
教師モデルがリスクの上限に与える影響
Knowledge Distillationについての一般的な定理
- が学生モデル。が真の分布。
- 学生モデルと教師モデルとUの分布について、それの誤差の二乗は右辺で抑えられる。
- 右辺の第一項は、Uデータの分布上での教師モデルの出力と真のラベル分布ののCross Entropyの分散である。
- 右辺の第二項は、教師モデルの出力分布と真の分布の2乗損失と、教師モデルのエントロピー。
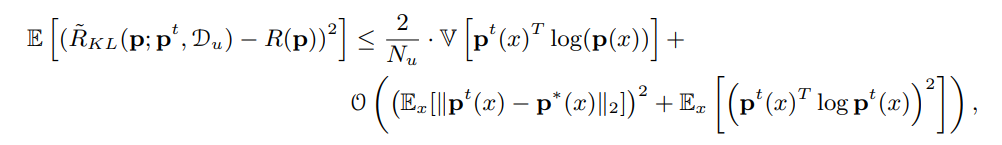
この結果からは、の数を大きくすると上界は小さくなるが、すべてを支配してるわけではない。特に真のモデルと教師モデルの分布の差は埋まりようがない。他には教師モデル(=真の分布)のエントロピーが大きければそれだけで上界が大きくなる。
KL Divergence下での提案手法の妥当性
上の定理で、を大きくすると、二項目のみ残るので、二項目を小さくしたい。
PT Lossを用いて計算することで、KL DivergenceがPT Lossとなるような教師分布という代理教師分布の存在を仮定する。(あるかもわからない)
あるかもわからないので、現実では以下のように最適化問題を解いていく。PT Lossで計算された値と、代理教師の出力分布と生徒のKL Divergenceができるだけ一致させるような、を求める。
下の数式で、とあるが、これは逆でという配置のほうが正しい。
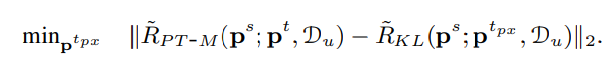
これはこのままでは解けないので、一つだけ妥協をする。を動かして最小化するというが、これが難しいので、まず「代理教師も学生は近くなるだろう」という仮定のもと、として代入をする。
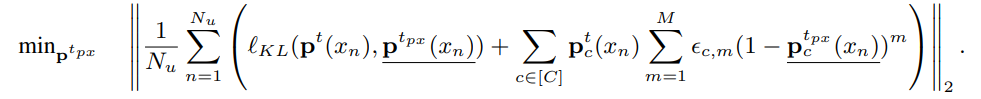
実際に最小化でを得るのは、すべての教師モデルの出力のlogitがあるので、それに対してこれを解くように数値計算で解く。
の選び方
は結論から言うと、ランダムに選ぶ。ランダムに選んだうえで、先ほどの定理のに依存しない項に対して計算し、最も小さい値をとるものとする。
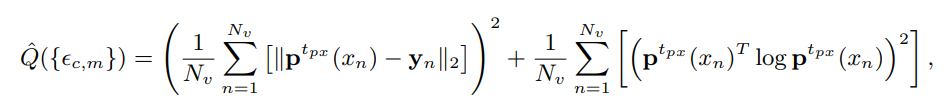
Experiments
- はまで展開しているらしい。
